Measurement of ABCD parameters of a long transmission line with magnitude and angle.

 Experiment: Measurement of ABCD parameters of a long transmission line with magnitude and angle.

Appratus: 

• variable Voltage Source (Variac) 230V AC with 2-Pole S/W
• No of π sections: 4 (100Km each)
• value of each component: Resistance = 4 Ohm; Capacitance = 0.47 microF; Inductance: 110mH.
• Voltmeter: 230 V AC (2 Nos)
• Ammeter: 5 A (2 Nos)
• Watt meter: 300V, 5A (1 Nos)

Theory:

ABCD Parameters of a Two Port Network

In any 4 terminal network, (i.e. linear, passive, bilateral network) the input voltage and input current can be expressed in terms of output voltage and output current. Each port has 2 terminals to connect itself to the external circuit. Thus it is essentially a 2 port or a 4 terminal circuit, having:

Given to the input port PQ.
Given to the output port RS.

Now the ABCD parameters of the transmission line provide the link between the supply and receiving end voltages and currents, considering the circuit elements to be linear in nature.

Thus the relation between the sending and receiving end specifications is given using ABCD parameters by the equations below.

Now in order to determine the ABCD parameters of the transmission line let us impose the required circuit conditions in different cases.

ABCD Parameters When Receiving End is Open Circuited

The receiving end is open-circuited meaning the receiving end current IR = 0.
Applying this condition to equation (1) we get,

Thus it’s implied that on applying open circuit condition to ABCD parameters, we get parameter A as the ratio of sending end voltage to the open circuit receiving end voltage. Since dimension-wise A is a ratio of voltage to voltage, A is a dimensionless parameter.

Applying the same open circuit condition i.e IR = 0 to equation (2)

Thus it’s implied that on applying open circuit condition to ABCD parameters of a transmission line, we get parameter C as the ratio of sending end current to the open circuit receiving end voltage. Since dimension wise C is a ratio of current to voltage, its unit is mho.

Thus C is the open circuit conductance and is given by
C = IS ⁄ VR mho.

ABCD Parameters When Receiving End is Short Circuited

Receiving end is short circuited meaning receiving end voltage VR = 0
Applying this condition to equation (1) we get,
Thus it’s implied that on applying short circuit condition to ABCD parameters, we get parameter B as the ratio of sending end voltage to the short circuit receiving end’s current. Since dimension wise B is a ratio of voltage to current, its unit is Ω. Thus B is the short circuit resistance and is given by
B = VS ⁄ IR Ω.
Applying the same short circuit condition i.e VR = 0 to equation (2) we get
Thus it’s implied that on applying short circuit condition to ABCD parameters, we get parameter D as the ratio of sending end current to the short circuit receiving end current. Since dimension wise D is a ratio of current to current, it’s a dimensionless parameter.

∴ The ABCD parameters of the transmission line can be tabulated as:

Parameter	Specification	Unit
A = VS / VR	Voltage ratio	Unit less
B = VS / IR	Short circuit resistance	Ω
C = IS / VR	Open circuit conductance	mho
D = IS / IR	Current ratio	Unit less

ABCD Parameters of Long T/L

What is Long Transmission Line?

A long transmission line is defined as a transmission line with an effective length more than 250 km (150 miles). Unlike short transmission lines and medium transmission lines, it is no longer reasonable to assume that the line parameters are lumped. To accurately model a long transmission line we must consider the exact effect of the distributed parameters over the entire length of the line. Although this makes the calculation of ABCD parameters of transmission line more complex, it also allows us to derive expressions for the voltage and current at any point along the line.

In a long transmission line the line constants are uniformly distributed over the entire length of line. This is because the effective circuit length is much higher than what it was for the former models (long and medium line) and hence we can no longer make the following approximations:

1. Ignoring the shunt admittance of the network, like in a small transmission line model.
2. Considering the circuit impedance and admittance to be lumped and concentrated at a point as was the case for the medium line model.

Rather, for all practical reasons, we should consider the circuit impedance and admittance being distributed over the entire circuit length as shown in the figure below. The calculations of circuit parameters, for this reason, are going to be slightly more rigorous as we will see here. For accurate modelling to determine circuit parameters let us consider the circuit of the long transmission line as shown in the diagram below.

Here a line of length l > 250km is supplied with a sending end voltage and current of VS and IS respectively, whereas the VR and IR are the values of voltage and current obtained from the receiving end. Lets us now consider an element of infinitely small length Δx at a distance x from the receiving end as shown in the figure where.
V = value of voltage just before entering the element Δx.
I = value of current just before entering the element Δx.
V+ΔV = voltage leaving the element Δx.
I+ΔI = current leaving the element Δx.
ΔV = voltage drop across element Δx.
zΔx = series impedance of element Δx
yΔx = shunt admittance of element Δx
Where, Z = z l and Y = y l are the values of total impedance and admittance of the long transmission line.

Therefore, the voltage drop across the infinitely small element Δx is given by

Now to determine the current ΔI, we apply KCL to node A.

Since the term ΔV yΔx is the product of 2 infinitely small values, we can ignore it for the sake of easier calculation.
Therefore, we can write

Now derivating both sides of eq (1) w.r.t x,

Now substitutingfrom equation (2)

The solution of the above second order differential equation is given by.

Derivating equation (4) w.r.to x.

Now comparing equation (1) with equation (5)

Now to go further let us define the characteristic impedance Zc and propagation constant δ of a long transmission line as

Then the voltage and current equation can be expressed in terms of characteristic impedance and propagation constant as

Now at x=0, V= VR and I= Ir. Substituting these conditions to equation (7) and (8) respectively.

Solving equation (9) and (10),
We get values of A1 and A2 as,

Now applying another extreme condition at x = l, we have V = VS and I = IS.
Now to determine VS and IS we substitute x by l and put the values of A1 and
A2 in equation (7) and (8) we get

By trigonometric and exponential operators we know

Therefore, equation (11) and (12) can be re-written as

Thus compared with the general circuit parameters equation, we get the ABCD parameters of a long transmission line as,

Evaluation of ABCD Constants:

This series converges rapidly for values of γl usually encountered for power lines and can be conveniently approximated as above. The corresponding expressions for ABCD constants are

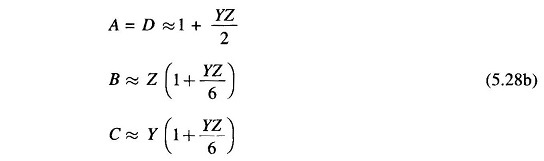
Circuit Diagram:

Fig. Experiment setup for Measurement of ABCD parameters of a long transmission line

Precaution:

• Use proper rated fuse
• The ground points of the equipment must be grounded firmly.
• Always keep the MCB to OFF state and the Variac to zero before conducting experiment.
• Make sure that the voltage rating does not cross 300V and current rating of 1 Amp.

Procedure:

1. Keep MCB in OFF condition & Variac in zero position.
2. Connect the circuit as shown in figure (Use n=4 no of Pi sections i.e. 400Km for long T/L ).
3. Make sure that circuit is connected properly and turn on supply.
4. Initially keep receiving and open circuit (connect voltmeter across point A and B shown in the circuit).
5. Set required voltage (Vs) and note down the quantities which are required for the practical as per the given observation table.i-e(Is,Vr,W). In this in this open circuit test Ir will be zero Amp.
6. reduce the input voltage to zero volt.
7. Now conduct short circuit test now connect ammeter across point A and point B.
8. Increase the input voltage. (keep input voltage in safe limit also make sure that current form sending inside and receiving and side should be below 1 ampere)
9. Note down the reading you will get Vs,Is,Ir,W.
10. In short circuit test Vr will be zero volt.
11. Note down both open circuit and short circuit readings in given observation table.
12. Calculate the equivalent ABCD parameters.

Observation Table:

Sr. no.	Condition	Vs	Is	W	Vr	Ir
1	Open circuit (Receiving end)	140	0.168	0	158	0
2	Short circuit (Receiving end)	82	0.432	0	0	1

*Above readings are for Example purpose

 Calculations:

Practically:

A= Vs/Vr(Ir=0 i.e OC Test) = 140/158= 0.89

B= Vs/Ir (Vr=0 i.e SC Test) = 82/1 = 82 ohm

C = Is/Vr(Ir=0 i.e OC Test) = 0.168/158 = 1.06*10^-3 mho

D = Is/Ir (Vr=0 i.e SC Test) = 0.432/1 = 0.432

Theoretically:

As we have,

Resistance = 4 Ohm; Capacitance = 0.47 microF; Inductance: 110mH....... per 100Km

Total length of 220 KV line is 400 Km.

so,

Impedance 

z=R+jωL

z= 4+j2π 50(110*10^-3)..........for 100km

Z_total=Z4₀₀₌ Total impedance of 400 km line;

Z= [4+j2π 50(110*10^-3)]*4

Z=16+j138.24

Z=139.16 ∠83.39^o

Admittance

y=g+jωC...............(for ease of calculation, conductance g is neglected)

y=jωC

y= j2π 50(0.47*10^-6)

y= j1.48*10^-4

_Ytotal=Y₄₀₀₌ Total Admittance of 400 km line;

Y= [j1.48*10^-4]*4

Y= j5.91*10^-4

Y= 5.91*10^-4∠90^o

Now, we can derive the ABCD parameters of a medium transmission line as:

A=D = ( 1 + YZ/2 )

=0.96+j4.734

=0.96∠0.28⁰

B = Z( 1 + YZ/6 )

=15.56+j136.38

=137.27∠83.48⁰

C = Y( 1 + YZ/6 )

= 3.24*10^-4∠180⁰

Results:

Sr. no.	Parameter	Practically	Theoretically
1	A	0.89	0.96∠0.280
2	B	82	137.27∠83.480
3	C	1.06*10^-3	3.24*10^-4∠1800
4	D	0.432	0.96∠0.280

Conclusion: Thus, we have calculated ABCD parameters of Long length T/L with magnitude and angle having length of 400 Km.